4.3 Yıldızların Gözlemsel Özellikleri

Yıldızların Uzaklıkları

Yıldızların bize uzaklıkları birbirinden çok farklıdır. Onların büyüklük gibi, toplam ışınımgücü gibi gerçek özelliklerini bulabilmek için önce uzaklıklarını bilmeliyiz. Şimdi en azından yakın yıldızların uzaklıklarının nasıl bulunduğunu görelim:

İşaret parmağınızı gözlerinizden 30 cm kadar uzakta tutunuz ve parmağınızın ucuna önce bir gözünüzle sonra diğer gözünüzle bakınız. Çok uzaktaki cisimlere göre parmağınızın ucunun belli bir açı kadar yer değiştirdiğini görürsünüz. Parmağınızı uzaklaştırdıkça yer değiştirme açısı da küçülür. Şimdi aynı işi çok uzaktaki bir cisimle yapınız; yer değişme olmadığını göreceksiniz. Yer değiştirme açısı, cismin gözünüzden uzaklığının bir ölçüsüdür.

Bu ilke genişletilerek, yıldızların uzaklığının bulunmasında kullanılır. Yer'in Güneş çevresindeki yörüngesini ve bu yörünge düzlemi içinde bir Y yıldızı ele alalım (Şekli 4.10), (Yıldız, Yer'in yörünge düzlemi içinde değilse ekliptik enleme bağlı formüller bunu hesaba katar.) Yer A konumunda iken Y yıldızı AY' doğrultusunda görülür. Altı ay sonra Yer B konumuna geldiği zaman aynı Y yıldızı bu kez BY" doğrultusunda görülür. Bir yıl sonra Y yine Y' doğrultusunda olacaktır. Güneşe çok uzak yıldızların yer değiştirmesi o kadar küçüktür ki A dan, G den ya da B den bakıldığında doğrultuları pek değişmez. Bu durumda XAY' ya da Y"BX' açısı ölçülebilir. Bu açı aynı zamanda AYG=p açısına eşittir. Bu açıya, Y yıldızının Güneş merkezli ıraklık açısı (paralaks) denir. Yani ıraklık açısı Yer -Güneş uzaklığını yıldızdan gören açıdır. AYG üçgeninde p açısı ve AG uzunluğu (Yer-Güneş uzaklığı) bilindiğine göre geometrik yöntemlerle,

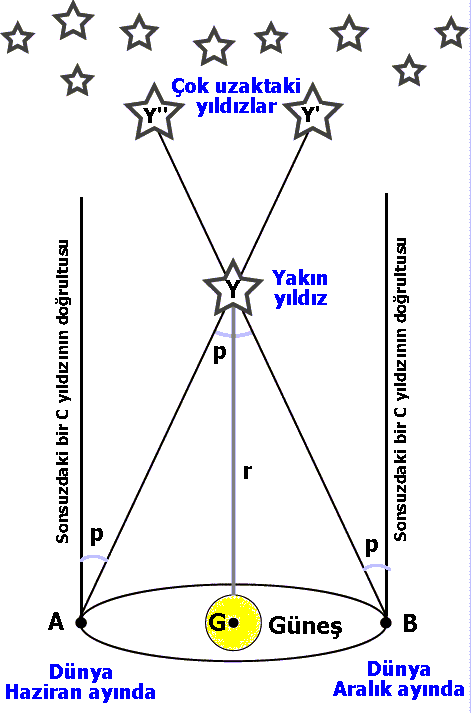
Şekil 4.10: Güneş merkezli ıraklık açısı. Y yıldızı, Yer A da iken Y' doğrultusunda, B de iken Y" doğrultusunda görülür.

yıldızın GY uzaklığı hesaplanabilir. Yıldızlar için p açısı her zaman 1 açı saniyesinden küçüktür. 1 saniyelik açı baş parmağınızın genişliğini 4 km uzaktan gören açıya eşittir. Böyle küçük açılı üçgenlerin çözümü daha da kolaydır. Yıldızlar için p açısı öyle küçüktür ki merkezi Y, yarıçapı yıldızın uzaklığı r ye eşit olan dairede, p yi gören yayın uzunluğunu Yer-Güneş uzaklığı AG ye eşit alabiliriz (Şekil 4.10). Bir dairede iki ayrı yay parçalarının uzunluklarının oranı, bu yayları gören merkez açılarının oranına eşittir. Dairenin çevresi 2πr ve bu çevreyi gören merkez açı 360° olduğuna göre (BG/2πr)=(p°/360°) yazılabilir. p küçük olduğu için açı saniyesi cinsinden ifade etmek âdet olmuştur. O zaman 360° yi de açı saniyesi cinsinden, yazmalıyız:

\F(AG,2πr) = \F(p",360x60x60)

r = \F(206 265 x AG,p")

AG = 1 GB (gök birimi) olduğuna göre, GB cinsinden,

r = \F(206 265 ,p") GB

olur ( " simgesi, açı saniyesi demektir). Astronomide 206265 GB uzunluğuna, 1 parsek denir ve kısaca pc yazılır. O zaman pc cinsinden r, basitçe r = 1/p parsek olur. O halde parsek, Yer-Güneş uzaklığını 1 açı saniyesi altında gören yıldızın uzaklığıdır, o da 206265 GB'ne eşittir. Kullanılan bir başka uzaklık birimi ışık yılıdır, bu ışığın bir yılda aldığı yoldur. 1 parsek = 3.26 ışık yılı olduğunu kolayca gösterebilirsiniz.

Dikkat edilirse, yıldızın uzaklığı (r) ne kadar büyükse ıraklık açısı (p) o kadar küçüktür. Bize en yakın yıldızın (Proxima Centauri) ıraklık açısı p = 0".75 dir; bu uzaklık için r = 1/0.75 = 1.33 parsek = 4.3 ışık yılı verir. Yani şu anda yıldızdan aldığımız ışık, 4.3 yıl önceki ışıktır.

Iraklık açılarının ölçülmesi çok zordur ve yıllar süren gözlemler gerektirir. Böyle küçük açıların ölçülmesine ölçü hataları karışmaktadır. Ölçülebilen en küçük açı 0".01 kadardır, bu 100 pc demektir. Bu yüzden 100 pc den daha ötedeki uzaklıklar için bu yöntem yararsızdır. Yer atmosferi dışından bakıldığında, atmosferin yıldız ışığını dağıtıcı özelliği ortadan kalktığı için (kıpraşma olmadığı için), daha küçük ıraklık açıları ölçülebilmektedir. Bu nedenle çok sayıda yıldızın ıraklık açısını ölçmek için yörüngeye uydu teleskoplar yerleştirilmiştir. Bu teleskoplarla 500 pc e kadar yıldız uzaklıkları ölçülebilmektedir. Halbuki gökte gördüğümüz yıldızların çoğu binlerce parsek ya da ışık yılı ötededirler. Samanyolunun çapı 100000 ışık yılı uzunluğundadır, diğer galaksiler ise milyonlarca, milyarlarca ışık yılı uzaktadır. Bütün bu uzaklıkları bulmada ıraklık açısına ayarlanan başka yöntemler kullanılır; bunların üzerinde durmayacağız.

Yıldızların Hareketleri

İçinde bulunduğumuz Samanyolu galaksisi çalkantılı, dönen bir kütledir. Güneş dahil bütün yıldızlar Samanyolu merkezi çevresinde müthiş hızlarla dolanırlar. Örneğin; yıldızların aşağıda anlatacağımız yöntemlerle ve başka yollarla hesaplanan uzay hızlarından, Güneş'in Samanyolu çevresinde yaklaşık 220 km/s hızla dolandığı bulunmuştur. Yıldızların yörüngeleri az ya da çok birbirlerinden farklıdır. Bizim yıldızımız Güneş'ten onları izlediğimizde, kimilerinin birbirine yaklaştığını, kimilerinin birbirinden uzaklaştığını görmeliyiz. Aynı şekilde kimisi bize yaklaşmalı, kimisi uzaklaşmalıdır.

Bir yıldızın Güneş'e göre hareketini, gökte uçan bir uçağın yerde duran bir gözlemciye göre hareketine benzetebiliriz. Uçak, genel olarak gözlemcinin bakış doğrultusuna eğik bir çizgi boyunca hareket eder. Bu hareketi, bir başka deyişle uçağın hızını, iki bileşene ayırabiliriz: Bakış doğrultusundaki hız ve bakış doğrutusuna dik doğrultudaki hız. Birincisine radyal hız, ikincisine teğetsel hız denir. Teğetsel hız, uçağın gökte görüldüğü doğrultunun, yani görüldüğü açının değişmesine neden olur. Uçak yakınsa, bu açı çabuk değişir ve uçak hızla geçer, uçak uzaksa uçağın (aynı zaman içinde) kat ettiği açı küçük olduğundan, uçağın yer değiştirdiği ilk bakışta sezilmeyebilir bile.

Yıldızlarda da ilke tam olarak aynıdır. Teğetsel hızın neden olduğu birim zamandaki açısal yer değiştirmeye, öz hareket denir.Yıldızın öz hareketi μ ve uzaklığı r ölçüldükten sonra teğetsel hızı V_t, basit trigonometriden hesaplanabilir (Şekil 4.11). μ ile V_t arasında,

V_t= 4.74 μ r = 4.74 \F(μ,p)

bağıntısı vardır; burada uzaklık r parsek biriminde, öz hareket μ ve ıraklık açısı p açı saniyesi birimindedirler. 4.74 sayısı, sonucu km/s birimine çeviren katsayıdır.

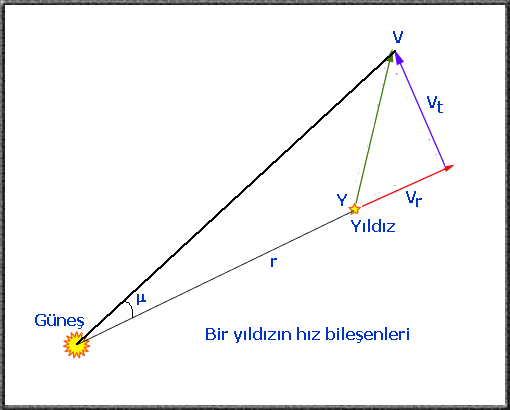
Şekil 4.11: Bir yıldızın güneşe göre hız bileşenleri: μ öz hareket, V_t teğetsel hız, V_r radyal (görüş doğrultusundaki) hız: V ise toplam hızdır.

Yıldızın radyal hızı V_r Doppler fomülünden bulunur (bkz. kesim 1.5). V_r ve V_t bilinince yıldızın Güneş'e göre uzay hızının büyüklüğü ve yönü, üçgende, dik açı bağıntılarından hesaplanabilir:

V\S(2, )=V\S(2,t)+V\S(2,r)

Öz hareket, yıldızın sağaçıklık ve dikaçıklığında değişmeye neden olduğundan, ilke olarak ölçülmesi kolaydır, fakat öz hareketler çok küçük olduklarından ölçülebilir büyüklüklere ulaşmaları için yıllarca beklemek, ölçtükten sonra da aradan geçen yıla bölmek gerekir. 10 yıl içinde 2".5 kayma gösteren bir yıldızın öz hareketi = 2".5/10 = 0".25 /yıldır. Öz hareketin varlığını ilk kez 1718 de Edmund Halley (şu kuyruklu yıldıza adını veren gök bilimci) keşfetti. Bugüne kadar on binlerce yıldızın öz hareketi ölçülmüştür. 300 den biraz fazlasının öz hareketi 1".0 /yıl dan büyüktür. Uzaklıklar büyük olduğu için bu öz hareketlerin çoğu yılda onda bir hatta yüzde bir açı saniyesinden küçüktür. En büyük öz hareket Barnard yıldızı adında bir yıldıza aittir: 10".25 /yıl; bu yıldız bize en yakın ikinci yıldızdır (Şekil 4.12).

Şekil 4.12: Barnard yıldızının öz hareketi. 1997 ile 2003 ve 2004 yılları arasında ne kadar yer değiştirdiğini göstermektedir. Bir yılda dahi ne kadar yer değiştirdiğini farkedebilirsiniz.