Eski Yunanlılar

Babilliler tarafından yapılan duyarlı ve uzun zaman aralıklarını kapsayan astronomik gözlemler eski Yunan astronomisinin temelini oluşturmuştur. Eski Yunanlılar, astronomik olaylardan çok onların nedenleri üzerinde durmuşlar ve ilk evren modellerini oluşturmuşlardır. Bu modellerde yıldızların tanrılara ilişkin mükemmel cisimler olduğu ve mükemmel hareketler yaptıkları kabul edilmişti. Eski Yunanlıların bu mükemmel hareket dedikleri, düzgün dairesel hareket var sayımıdır. Kepler zamanına kadar astronomik düşüncenin vaz geçilmeyen bir var sayımı olarak kalmıştır.

Eski Yunanlıların bildiğimiz ilk doğa filozofu Tales'e (M.Ö. 640-546) göre Yer, suda yüzen yassı bir diskti. Tales gezegenlerin ve yıldızların hareketleri hakkında hiç yorum yapmamıştı. Tales'in çağdaşı Anaksimander (M.Ö. 611-547) ise Yer'in uzayda yüzen bir silindir olduğunu ileri sürmüştür. M.Ö. 6. yüzyılda birbirinden bağımsız iki okul oluşmuş. Bunlardan Xenophanes (Senofanes) (M.Ö. 570-500) okuluna göre Yer, düz ve sonsuz boyuttaydı. İkinci Pitagor (Pisagor) (M.Ö. 580-500) okulu daha çok gözlemlere dayanıyordu. Pitagor, Yer üzerinde yaptığı uzun yolculuklar sonunda onun küre biçimli olduğuna inanmıştı. Yer'in yuvarlak olduğuna inandıkları halde bu okuldan hiç kimse onun döndüğünü savunmamıştı. Bu okula göre 10 sayısı 1+2+3+4=10 olduğu için mükemmeldi. O zaman 9 farklı gök cismi (Yer, Ay, Güneş, beş gezegen ve sabit yıldızlar) gözleniyordu. Mükemmellik ve simetri nedeniyle bu sayı 10 olmalıydı. 10. cisim olarak Yer'in bir eşi olduğunu ileri sürdüler. Yine bu okula göre 10 farklı gök cismi Yer'in eşi tarafından örtüldüğü için hiç görünmeyen bir ateş merkezi etrafında yörünge hareketi yapmaktaydı. Bu görüşe göre Yer, ilk kez yörünge hareketi yapan bir gezegen olarak dikkate alınmıştı.

M.Ö. 467 yılında Yunanistan'a düşen demirli gök taşının Güneşten geldiğini düşünen Anaxagoras (Anaksagoras) (M.Ö. 500-428) Güneş'in yakın ve Yunanistan'ın bir parçası kadar küçük olduğunu, maddesinin de erimiş demir olduğunu düşündü; Anaxagoros'a göre Yer, düzdü; Ay'ın büyüklüğü Güneş'inki kadardı ve Ay, Güneş ışığını yansıtıyordu. Anaxagoras bu görüşleriyle cezalandırılmak istenmiş, Perikles tarafından ölümden kurtarılarak sürgüne gönderilmiştir.

Daha sonraki dönemin önemli bir okulu Plato (Eflatun)'nun (M.Ö. 427-347) adını taşır. Plato kendisi Pitagor okulundan etkilenmiş ve o okulun görüşlerini geliştirmiştir. Evrende geometrik bir düzenin varlığına inanmış ve yedi gök cismi için inandığı göreli uzaklıkları (Ay-1, Güneş-2, Venüs-3, Merkür-4, Mars-8, Jüpiter-9, Satürn-27); 1, 2, 4, 8 ve 1, 3, 9, 27 şeklindeki iki geometrik seriyle göstermiştir. Plato, Pitagor okulunun inandığı gök cisimlerini taşıyan ve görünmeyen müzikli kristal küreler kavramına da inanmış ve onu geliştirmiştir. Anlaşıldığına göre Plato, gök cisimlerinin günlük görünür hareketlerinin Yer'in dönmesinden kaynaklandığına inanmıştır.

Yaygın olan Plato (Eflatun) okulunun görüşü, Yer'in diğer bütün gök cisimlerinden farklı olduğunu ve onun evrenin merkezinde olması gerektiğini öngörüyordu. Yer merkezli evren modelini eski Yunan'da ilk kez Eudoxus (Eudoksus) (M.Ö. 408-355)'un ileri sürdüğünü görüyoruz. Eudoxus'a göre Ay, Güneş ve bilinen 5 gezegen sabit olan Yer etrafında aynı merkezli çemberlerde dolanırlar. İkincil küre (epicycle) kavramını da gezegenler kuramına sokan Eudoxus'tur. Eudoxus, geliştirdiği modelin gözlemleri tam sağlamadığını görünce, Philolaos (Filolaus)'un var saydığı görünmeyen küreler üzerinde daha küçük ve görünmeyen başka kürelerin var olabileceğini düşündü. Ona göre gezegenler bu ikincil küreler üzerinde bulunuyorlardı. Eudoxus'un evren modelinde görünmeyen toplam küre sayısı 27 dir. Daha sonradan desteklenip Galluppus, Aristo, Hipparchus (Hiparkos) ve Ptolemy (Arap dünyasında Batlamyus olarak bilinir) tarafından geliştirilen bu Yer merkezli modelde gezegenlerin karmaşık görünür hareketleri kolayca açıklanabiliyordu fakat gözlemlerin duyarlılığı arttıkça modelden olan sapmaları açıklayabilmek için ikicil küre sayısını arttırmak gerekiyordu. Endoxus'a inanan Aristo, (MÖ. 384-322) sadece filozofik nedenlerle ikincil küre sayısını 55'e çıkarmıştı. Aristo o günün bilgisine uygun kanıtlarla Eudoxus modelini inandırıcı bir şekilde savunmuştur. Yer'in yörünge hareketi yapmış olması hâlinde yıldızların paralaktik hareket yapması gerektiğini, böyle bir hareket gözlenmediği için de Yer'in merkezde durağan olması gerektiğini savunmuştur. Söz konusu paralaktik hareketin gözlenememesinin nedenini daha sonra Aristarchus (M.Ö. 310-230) açıklamıştır.

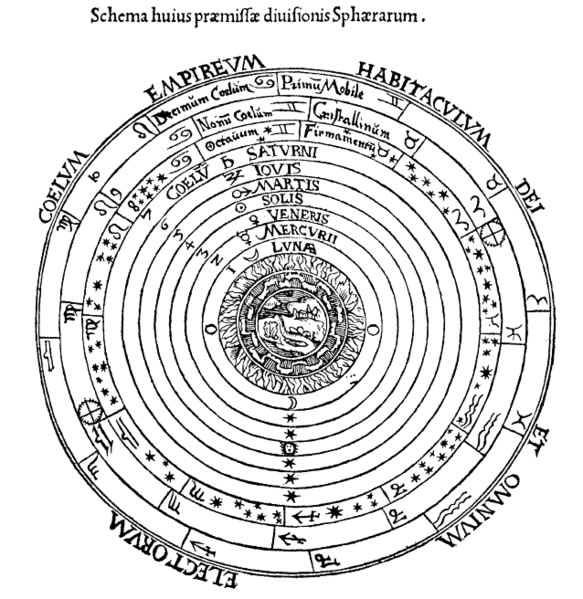
Şekil 2.5: Eski Yunanistan'da; Plato, Aristo, Hipparchus ve Batlamyus okullarının inandığı Yer merkezli evren modeli. Gezegenlerin burada gösterilmeyen ikincil çemberler (epicycle) üzerinde hareket ettiğine inanılmıştır.

Aristo, Yer'in çok büyük bir küre olduğunu iki önemli kanıtla göstermiştir. (i) Ay tutulması sırasında Yer'in Ay üzerindeki gölge sınırının geniş bir yay olması ve (ii) Yer üzerinde güneye gidildikçe yeni yıldızların görünür olması. Aristo, kutup ışıması, akan yıldız ve kuyruklu yıldızların Yer'in üst atmosferindeki olaylar olduğunu ileri sürmüştür. Aristo döneminde yaşayan Heraklit (M.Ö. 388-315) küresel Yerin bir eksen etrafında döndüğünü, evrenin sonsuz olduğunu Merkür ve Venüs'ün Güneş etrafında döndüğünü ileri sürmesine karşın Aristo'nun inandırıcı kanıtlarla süslediği filozofik görüşleri tutunmuş, yaygınlaşmış ve etkilerini Avrupa' da rönesans dönemine kadar sürdürmüştür. Aristo zamanlarında bilinen 5 gezegen (Merkür, Venüs, Mars, Jüpiter ve Satürn), Ay ve Güneş sihirli 7 sayısını oluşturuyordu. Yer, o zaman gezegen sayılmıyor ve ona her bakımdan büyük bir ayrıcalık tanınıyordu. Yer'in etrafında 7 gök cismine ilişkin 7 görünmeyen kristal küre evreni 7 katmana ayırıyordu. Tek tanrılı dinlerin kutsal kitaplarında sık sık sözü edilen "7 kat gök" kavramı buradan gelmektedir. Haftanın 7 gün olması da aynı kaynaklıdır. Hatta müzik notalarının kaynağı da 7 katlı evren modeliyle ilgilidir. O zamanki inanışa göre 7 gök cismini taşıyan 7 büyük görünmez küre kristalden yapılmış olmalıydı ve dönerlerken çıkardıkları ses günahlarından arınmış kişilerce duyulabilmekteydi. Eski Yunan'da bu tür kişilerin duydukları sesleri taklit etmeleriyle yedi kristal kürenin çıkardığı ses olarak yedi temel müzik notası ve ikincil kürelerin sesleriyle de bemoller, diyezler ortaya çıkmış oldu.

Aristo'dan yüzyıl kadar sonra Samos'lu Aristarchus (M.Ö. 312-230), ilk kez Güneş merkezli bir evren modeli ileri sürmüştü. Aslında Aristo da Güneş merkezli modeli tartışmış fakat yıldızların beklenen paralaktik kayması gözlenemediği için modelin doğru olmadığına karar vermiştir. Aristarchus'a göre paralaktik kayma gözlenemiyordu; çünkü yıldızları taşıyan küre o kadar büyüktü ki Yerin yörüngesi onun yanında çok küçük kalıyordu. Aristarchus tam ilk dördün evrdesinde Ay'ın uzanım açısını 87° ölçerek Ay-Yer ve Güneş'in oluşturduğu dik üçgenden Güneş uzaklığını, Ay uzaklığının 20 katı bulmuştur. Diğer taraftan Ay ve Güneş'in görünür çaplarının eşit olduğunu dikkate alarak Güneş'in Ay dan 20 kat daha büyük olması gerektiğini düşünmüştür. Burada izlenen yol doğru olduğu hâlde, açı ölçümündeki hatalar nedeniyle sonuçlar yanlıştır. Aristarchus, tutulma gözlemlerinin geometrisinden Ay ile Yer'in yarıçaplarını da karşılaştırmış ve R_Yer= 3 R_Ay bulmuştur. Aristarchus Güneş'i, büyüklüğü nedeniyle, evrenin merkezine koyup Güneş merkezli modeli savunmuş olabilir.

Ayrıca bu dönemde ilk kez Eratosthenes (M.Ö. 273-192) tarafından küre biçimli kabul edilen Yer'in yarıçapı ilginç bir yöntemle doğruya çok yakın olarak bulunmuştu. 22 Haziran günü Güneş Syene kentinin başucu noktasında bulunduğu anda, İskenderiye kentinde Güneş'in başucu uzaklığı 7.2 açı derecesi ölçülmüş, ve bu açının Syene-İskenderiye arasındaki uzaklığı gören merkez açıya eşit olduğu dikkate alınarak (bkz. Şekil 2.7 ),

S = q(rad) x R

genel bağıntısında 7.2 derecelik merkez açı (q) nın radyan değeri ve bu açının gördüğü Syene-İskenderiye uzaklığı (S) yerine konarak Yer'in yarıçapı R=6405.26 km bulunmuştur. Bu, bugünkü ortalama gerçek değer 6370 km ye çok yakındır. Bu bulguyla birlikte tutulmaların geometrisinden yararlanılarak Ay ve Güneş'in uzaklıkları ve büyüklükleri tahmin edilmiştir. Güneş'in görünür hareketindeki düzensizlikler farkedilmiş, Ay'ın yörüngesiyle ekliptik çemberi arasındaki 5 açı derecesi olan açı ölçülmüştür.

Şekil 2.6: Güneş merkezli Aristarchus evren modeli. Kopernik 17 yüzyıl sonra aynı modeli savunmuştur.

Hipparchus (M.Ö. 190-125) zamanında gezegen parlaklıklarının yıl boyunca değiştiği biliniyordu. Hipparchus buradan gezegen-Yer uzaklığının yıl boyunca değişmesi gerektiğini düşünerek Yer merkezli modelde Yer'in görünmeyen kürelerin tam merkezinde olmaması gerektiğini savunmuştur. Hipparchus, hazırladığı yıldız kataloğundaki yıldız konumlarıyla aynı yıldızların daha önceden kaydedilen konumlarını karşılaştırarak konumlarda sürekli fakat çok yavaş olan bir değişimi farketmiştir. Hipparchus'un astronomiye asıl katkısı, bugün kullanılan yıldız parlaklıklarının ölçüm sistemini geliştirmiş olmasıdır.

Daha sonra Ptolemy (M.S.100-170), evren modeli konusunda Hipparchus'u örnek alarak Yer merkezli evren modelini kabul etmiştir. Gezegenlerin kavuşum dönemlerini belirlemiş ve onların Yer'e uzaklıklarını geometrik yollarla hesaplamıştır. Ptolemy'nin astronomiye en önemli katkısı yazdığı 13 çiltlik astronomi kitabıdır. Ptolemy, Arap dünyasında Almagest olarak adlandırılan bu kitabında zamanının tüm astronomi bilgisini toplamıştır. Hipparchus'un yıldız kataloğunu da kapsayan bu kitap yüzyıllarca temel astronomi kitabı olarak kullanılmıştır. Hipparchus'un yıldız kataloğu, gözle görülebilen yıldızların o zamanki parlaklık ve koordinatlarını vermesi bakımından önemlidir. Aynı yıldızların bugünkü koordinatları Hipparchus kataloğundaki değerlerle karşılaştırılarak o yıldızların öz hareketleri ve ayrıca, varsa, çok uzun dönemli parlaklık değişimleri bulunabilmektedir.

Milattan sonra birkaç yüzyıl içinde Hristiyan'lığın hızla yayılması ve daha sonra da Roma İmparatorluğu'nun çökmesiyle Avrupa'da bilime verilen önem hemen hemen tamamen ortadan kalkmış, Aristo düşüncesinin kiliseye yerleşmesi ile de Avrupa karanlık bir döneme girmiştir.

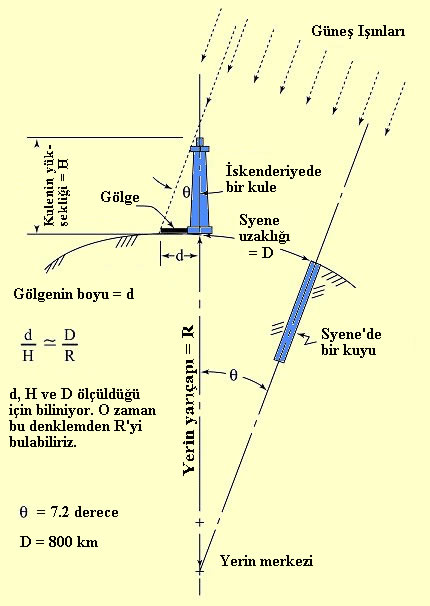
Şekil 2.7: Erathosthenes'in yerin yarıçapını ölçmesi.